Introduzione
Il muone nel modello standard fa parte dei leptoni, le particelle "leggere" come gli elettroni. Quando Anderson e Neddermeyer nel 1936 scoprirono questa nuova particella di massa intermedia tra l'elettrone e il protone per diverso tempo essa non ebbe una definizione uniforme e nei documenti storici si può trovare descritta come dynatron, penetron, barytron, heavy electron, yukon e x-particle [1]. La definizione ufficiale alla fine fu quella di mesotrone o mesone-µ (mu), ma nella fisica moderna questa definizione non è più valida e il termine corretto è semplicemente quello di muone.
Il muone fa parte delle particelle di seconda generazione il che significa che è instabile ed entro breve tempo deve trasformarsi o decadere, inizialmente era stata ipotizzata la possibilità che il muone fosse uno stato eccitato dell'elettrone e che potesse decadere in e+γ, questo tipo di decadimento non è mai stato osservato a conferma del fatto che il muone è una particella a sé. Il canale di decadimento tipico è invece quello | e + υe + υµ | (un elettrone e due neutrini) e il tempo medio di decadimento è di 2.2 µs (vedi anche la pagina di introduzione alle astroparticelle).
Il muone è stato utilizzato come "orologio" per provare la teoria della relatività speciale di Einstein. Il muone infatti, prodotto intorno ai 15000 metri di altitudine e vivendo solo 2.2 micro-secondi, anche se viaggiasse alla velocità massima possibile c (velocità della luce) potrebbe percorrere solo circa 600 metri e quindi non dovremmo trovare muoni a livello del mare. La relatività di Einstein prevede che viaggiando alla velocità della luce il tempo rallenta di un fattore γ detto fattore di Lorentz oppure che lo spazio si accorcia in relazione allo stesso fattore γ.
t'=t·γ (1), l'=v·t·γ (2), dove:
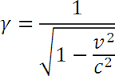
il rapporto v/c è definito anche β
Lo scopo delle trasformazioni di Lorentz, al pari di quelle di Galileo è mettere in relazione le coordinate di spazio e tempo di un evento che si verifica in due sistemi di riferimento, uno in moto rispetto all'altro.
Le trasformazioni tra sistemi di riferimento furono calcolate anche da altri autori (come FitzGerald), ma non furono ideate espressamente per la relatività. Anche la famosa relazione E=mc2 sembra sia stata scritta qualche anno prima di Einstein in diverse forme come ad esempio E=3/4mc2 (Fritz Hasenohrl)[2] in relazione all'energia di corpo nero. A quei tempi tuttavia non era una convenzione citare il lavoro di altri, comunque sia fu Einstein a sistemare le cose e a capire che le trasformazioni di Lorentz erano perfette per la sua legge della relatività speciale.
La prova sperimentale della relatività speciale fu messa in pratica nel 1940 - grazie al flusso dei muoni - da Bruno Rossi e David B. Hall e pubblicata nel 1941 sul Physical Review. Il flusso di muoni fu misurato a Echo Lake a 3200 metri di quota (Mount Evans) e a Denver (circa 1600 metri di quota). Rossi e Hall trovarono che, senza considerare gli effetti relativistici, il flusso di muoni a Denver era molto più alto di quello atteso.
L'esperimento della dilatazione del tempo
L'esperimento generalmente consta di due fasi, una fase in alta montagna ed una fase a quota inferiore o a livello del mare.
In entrambi i casi si tratta di selezionare un gruppo di particelle che abbiano il medesimo momento (p), questo si traduce posizionando uno spessore di materiale assorbente sopra alla strumentazione. In questo modo tutti muoni entro un certo range di energia (definito appunto dallo spessore di assorbente) rallenteranno e si fermeranno nel rivelatore. Particelle con un momento inferiore verranno assorbite e quelle con momento superiore continueranno il loro viaggio.
Tale rivelatore deve avere una dimensione sufficiente da permettere di rivelare due segnali prodotti dal muone: quello del suo arrivo e quello di decadimento (per essere sicuri che si sia fermato nel rivelatore). Il tempo trascorso tra questi due segnali corrisponde al tempo di decadimento del muone.
Ottenuti i dati nella prima fase ad alta quota, l'esperimento deve essere poi riprodotto a livello del mare. Il confronto tra i dati ottenuti nelle due esperienze dimostreranno che:
Questo dimostra la validità della teoria della relatività speciale o ristretta di Einstein (quella generale è un'altra storia).
Noi umani non risentiamo direttamente degli effetti relativistici perchè ci spostiamo a una velocità molto inferiore a quella della luce, le particelle elementari che si muovono vicino alla velocità "c" invece risentono degli effetti, tanto che la loro massa sembra aumentare, sempre in funzione del fattore di Lorentz:
m=m0·γ,
cioè la massa totale corrisponde alla massa a riposo moltiplicato per γ, quindi:
E=m·c2 si può scrivere E=m0·γ·c2
Grazie a questa relazione (e al valore di massa a riposo del muone, allora già noto) Rossi e Hall poterono calcolare che un muone da 500 MeV di energia viaggia con una velocità pari a 0.99 c [3].
In effetti se applichiamo i dati:
E=m0·γ·c2 = 500MeV/c2 = 107MeV·γ·c2 --> γ = 500/107 = 4.67 --> β=0.98
Se ora applichiamo la (1) vista prima t'=4.67·2.2 = 10.27 µs
ne segue che applicando la (2) l' = 3·108·0.98·10.27·10-6 = 3019 m
Questo significa che un muone fermato a Echo Lake da Rossi poteva tranquillamente arrivare a livello del mare prima di decadere.
Un'altra interessante caratteristica che emerge dalla relatività è che il rapporto tra la distanza percorsa e l'energia l/E è costante ed è di 4.5 km per GeV [3], questo spiega perchè per raggiungere il livello del mare, i muoni devono inizialmente avere (creati a circa 16 km) un'energia minima intorno ai 3 GeV.
L'esperimento dal punto di vista didattico
Questo interessante esperimento è stato riprodotto da diversi autori, come quello del Monte Washington che riportiamo nel video a fondo pagina. Spesso ci è stato chiesto se sia possibile ripetere questa esperienza con i rivelatori didattici (sia a GMT che a PMT) come l'AMD5, la risposta è purtroppo negativa in quanto il setup dell'esperimento (come riportato in seguito) è piuttosto complesso, tuttavia si possono fare esperimenti alternativi come quello proposto in questa pagina. In assenza di un rivelatore ci possiamo divertire a fare qualche simulazione con questa applet:
...purtroppo eliminata dall'autore, altra risorsa qui...
Simulatore dell'esperimento di Rossi - Hall, e altri [4]
Per dimostrare quanto sia complessa l'impostazione dell'apparecchiatura di rilevazione riportiamo uno dei primi esperimenti effettuato con i tubi di Geiger e Müller (GMT). Questa prima misura sperimentale attuata per trovare il tempo di decadimento del muone è stata condotta da Franco Rasetti in Canada con l'aiuto di Paolo Pontecorvo (fratello del più famoso Bruno) sempre nei primi anni quaranta. L'apparato sperimentale ideato e costruito da Rasetti è riportato qui sotto:
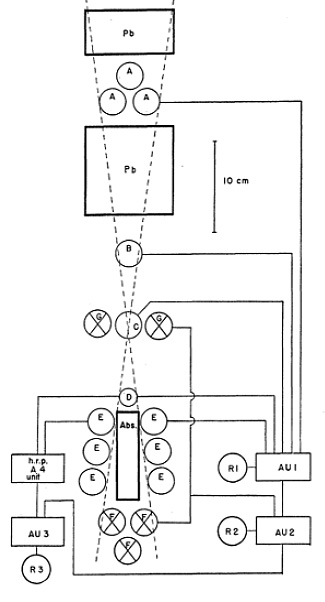
(Physical Review 77, p102 -1949)
L'apparecchio comprende una ventina di tubi GMT (i cerchi A,B,C,D...). I muoni vengono prima rallentati da blocchi di piombo o ferro e identificati dalla coincidenza di A B e C, il gruppo F invece serve in anti-coincidenza per controllare che il muone non sia uscito dall'apparato. Anche i tubi G sono in anti-coincidenza per non considerare muoni decaduti troppo presto e che hanno generato secondari nel piombo. I tubi E servono per rivelare elettroni prodotti dal decadimento dei muoni. Rasetti aveva ottenuto prima una misura del tempo di vita media di 3 µs (+-1.5) e poi con l'apparato migliorato, una più precisa misura di 1.5 µs (+-0.3), Rossi e Hall invece misurarono un valore di 2.4 µs (+-0.3), non molto distante dagli attuali 2.2 µs.
Questo setup rimase praticamente invariato per diversi anni solo che i GMT furono progressivamente sostituiti da scintillatori accoppiati a PMT (fotomoltiplicatori).
Video dell'esperimento sul monte Washington
[1] CARL D. ANDERSON & SETH H. NEDDERMEYER, Mesotron (Intermediate Particle) as a Name for the New
Particles of Intermediate Mass, Nature 142, 878-878 (12 November 1938).
[2] arXiv:1108.2250 [physics.hist-ph]
[3] Alberto Bandini Buti, La relatività, Sandit 2007
[4] http://www.kcvs.ca/site/projects/specialRelativity.html
- pagina sotto revisione -
M.A.

Collegamento tra meteo spaziale e cambiamenti atmosferici con i raggi cosmici 27.02.2026
Le condizioni atmosferiche sopra l'Antartide influenzano i cicli climatici globali e sono quindi fondamentali per la valutazione del clima. Tuttavia, studiare i cambiamenti atmosferici in Antartide è piuttosto impegnativo, poiché sono guidati da una varietà di processi su scala locale non facilmente catturabili dai modelli globali. Il monitoraggio delle variazioni stagionali della pressione atmosferica è un modo per tenere traccia dell'evoluzione dell'atmosfera antartica. Con il loro modello, gli autori dimostrano che i rilevatori di raggi cosmici Cherenkov ad acqua possono essere utilizzati in modo affidabile come indicatori delle variazioni della pressione atmosferica, aggiungendo così un nuovo strumento semplice ed efficace per monitorare e studiare le dinamiche della bassa stratosfera sopra l'Antartide...
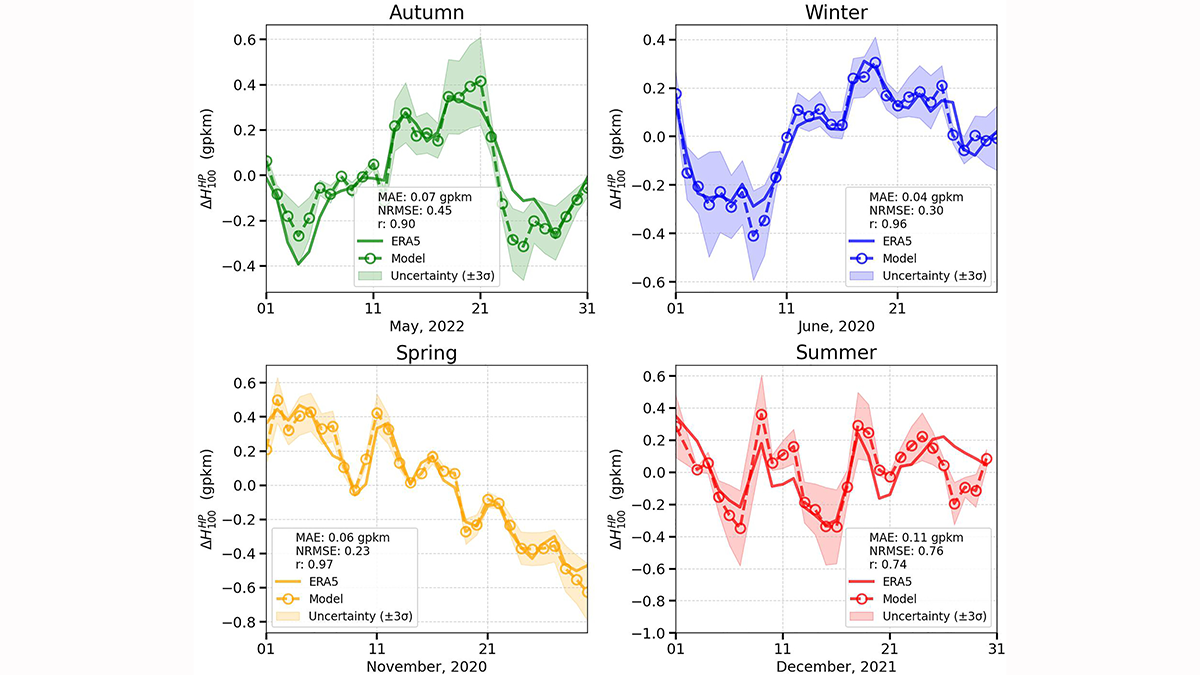
Fonte: EOS
Il libro AstroParticelle
26.09.2013 - Un viaggio scientifico tra i raggi cosmici raccontato attraverso la storia, le invenzioni i rivelatori e gli osservatori; senza trascurare gli effetti che essi producono coinvolgendo numerose discipline scientifiche tra cui astrofisica, geofisica e paleontologia.
Accedi | Registrati