I muoni sono particelle subatomiche prodotte in atmosfera in seguito al costante bombardamento dei raggi cosmici provenienti dallo spazio. La produzione avviene ad alta quota e il massimo di intensità è misurabile coi palloni stratosferici tra 15-17 km di altezza. Queste particelle però sono instabili e la durata della loro vita è brevissima, tanto che potrebbero fare solo qualche centinaio di metri per poi svanire trasformandosi in un elettrone e una coppia di neutrini, di fatto senza mai raggiungere il suolo terrestre. Nonostante ciò invece i muoni li misuriamo ovunque, persino in caverne a diversi centinaia di metri sottoterra. Non è facile spiegare questo fatto finché non si pensa che le particelle si muovono quasi alla velocità della luce e quindi subiscono degli effetti di dilatazione temporale o di contrazione spaziale che solo una teoria riesce a spiegare. Misure sul flusso di raggi cosmici ottenute per mezzo di semplici rivelatori di muoni permettono di valutare gli effetti previsti dalla teoria della relatività speciale di Einstein.

La dimostrazione degli effetti di dilatazione spiegati dalla relatività speciale richiede complesse strumentazioni in grado di selezionare un gruppo di muoni che abbiamo lo stesso momento, per fare questo è necessario misurare il loro tempo di decadimento e contarne il numero, un lavoro non certo semplice. Questa è una pratica che si può adottare in università, di solito con alcuni limiti. In questo intento didattico adatto anche a studenti delle scuole secondarie di secondo grado lo scopo si raggiunge applicando alcuni presupposti e un po’ di matematica “creativa”. Una dimostrazione semplificata degli effetti relativistici si ottiene costruendo un modello matematico per il comportamento atteso dei muoni cosmici in atmosfera e confrontandolo con il comportamento dell’intensità dei muoni realmente misurata. L’impalcatura necessaria per affrontare questo argomento riguarda fisica delle particelle, relatività speciale, decadimenti radioattivi, e ovviamente fisica dei raggi cosmici.

A sinistra il rivelatore AMD11, a destra una versione portatile del rivelatore AMD5.

I muoni nella fisica delle particelle elementari

Iniziamo dalla prima materia per ricavare le caratteristiche fisiche necessarie. Il muone per il modello standard delle particelle elementari è una particella di seconda generazione ed è considerato il cugino dell’elettrone perché è molto simile, esso ha una carica elettrica, e interagisce per forza elettromagnetica e nucleare debole (e gravitazionale). La sua massa tuttavia è molto maggiore ed equivale a 105,7 MeV/c2 a differenza dei 0,511 MeV/c2 dell’elettrone. Le particelle in movimento acquisiscono energia cinetica e l’energia totale di una particella è data dalla somma tra la sua energia a riposo (la massa) e la sua energia cinetica. Un primo presupposto è che per questo studio dobbiamo considerare solo muoni con energia cinetica prestabilita, ad esempio 6 GeV, che è un valore grande, ma presumibilmente reale per molti dei muoni che si generano in atmosfera oltre i 16 km di altitudine.

La relatività

La formula più famosa della storia è quella che lega energia e massa di una particella ovvero E=mc², tuttavia tale relazione è piuttosto incompleta in quanto vale solo per particelle immobili, anzi si può dire che definisce solamente l’energia per una particella a riposo. Per una particella in moto e con velocità prossime a quelle della luce deve essere introdotto un parametro di correzione chiamato fattore di Lorentz (γ). Il fattore di Lorentz ci serve per calcolare la velocità dei muoni e per costruire il nostro modello matematico ed esso equivale al rapporto tra l’energia totale e l’energia a riposo della particella, per i nostri muoni γ=57.6. Per una particella relativistica la velocità si ottiene da una relazione derivata dal framework relativistico, coi nostri dati v=0.9996c = 299747275 m/s

Radioattività

Le particelle di seconda generazione sono instabili, questo significa che la vita del muone è determinata e in media è pari a 2.2 μs. Trascorso questo breve lasso di tempo il muone scompare trasformandosi in un elettrone e in una coppia di neutrini. Il fatto che i muoni siano instabili ci introduce alla terza disciplina, in effetti si può dire che il muone è radioattivo e come qualsiasi elemento instabile o radioattivo decade dopo un certo tempo. Il tempo di vita per i muoni è ciò che in radioattività viene definito “vita media”. Il reciproco della vita media è invece definito costante di decadimento (λ) e per i muoni è facile valutare che vale: λ=4.5∙10⁵ si può quindi dire che in un secondo decadono un numero di muoni pari a λ. Facendo parte degli elementi radioattivi i muoni seguono anche la legge del decadimento radioattivo N(τ)=N(0)e^(-λτ) , questo significa che gli atomi e le particelle radioattive sono sottoposte a una diminuzione esponenziale nel corso del tempo. Se ad esempio immaginiamo un elemento radioattivo racchiuso in una scatola: N0 è il numero di atomi instabili (isotopi radioattivi) iniziale di quell’elemento; λ è la costante di decadimento che è diversa per ogni elemento considerato; N(τ) è il numero degli atomi rimanenti che troveremmo dopo un certo tempo nel campione all’interno della scatola; τ è appunto il tempo trascorso considerato. Per i muoni è un po’ più complicato perché non possiamo intrappolarli in un contenitore e attendere il loro decadimento, ma si generano e svaniscono continuamente in modo dinamico, tuttavia come secondo presupposto possiamo considerare che il numero di muoni a 16 km di quota sia in media costante e che quindi costituisca il nostro N0. Rimane da capire come fare a contare tali muoni e dare un valore a N0. Questo è ovviamente molto difficile, se non impossibile, ma nemmeno ci serve saperlo se introduciamo il terzo presupposto, dicendo che i muoni che piovono in verticale e che misuriamo con un rivelatore in un punto qualsiasi al suolo sono proporzionali al valore dei muoni N0, ovvero N0∝Nz e quindi Nz=k∙N0 ,ma per semplificare ulteriormente consideriamo k=1 (oppure un valore arbitrario che possiamo riprendere al termine).

Fisica dei raggi cosmici

Nella fisica dei raggi cosmici, un effetto fisico noto è quello della perdita di energia dipendente dall’angolo di inclinazione con cui i muoni attraversano l’atmosfera. Questo effetto è misurabile con un rivelatore ed è anzi diventata una misura popolare come attività didattica. La misura consiste nell’orientare il rivelatore su angoli diversi per intercettare i muoni aventi diverso angolo di inclinazione rispetto allo zenit. Il fenomeno segue la relazione: Iθ=Iz∙cos²θ Per il momento comunque ignoriamo di conoscere questa relazione e iniziamo invece a ragionare sul modello per verificare la relatività speciale attraverso la misura dell’inclinazione rispetto allo zenit.

L’altezza considerata è di 16 km, un muone prodotto a tale quota e diretto a terra con angolo di inclinazione nullo farà esattamente 16.000 metri di strada, mentre un muone con un certo angolo di inclinazione farà più strada, se “s” è la lunghezza per i muoni con θ=0, allora sθ=s/cos⁡θ, (figura 1) tuttavia per creare il nostro modello matematico possiamo considerare solo lo spazio eccedente che i muoni devono attraversare rispetto alla lunghezza s, in modo che sδ=s(1/cos⁡θ -1)

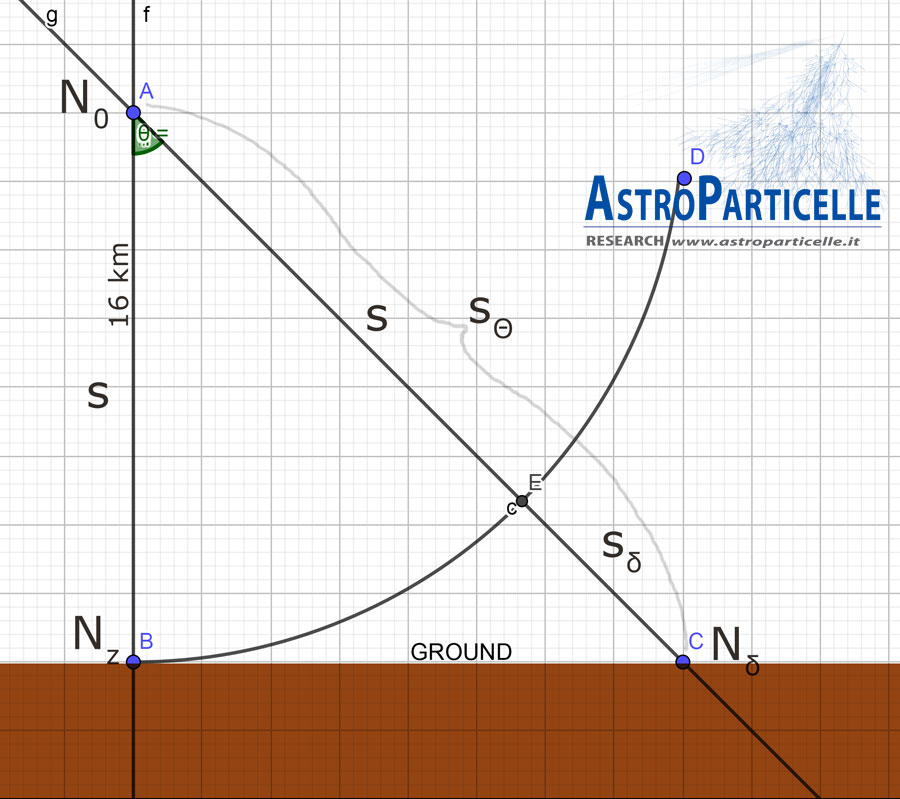
Il modello matematico

A questo punto prendiamo la formula per il decadimento radioattivo e vediamo come scriverla applicando i dati in nostro possesso, prima per una geometria euclidea e poi corretta per gli effetti relativistici dove la lunghezza sδ si contrae per gli effetti delle trasformazioni di Lorentz: s(δ,r)=sδ √(1-β^2 ) Il modello è fondato sul fatto che i muoni inclinati in atmosfera fanno più strada e perciò nell’attraversare lo spazio sδ un certo numero di muoni subirà il decadimento previsto, quindi il numero di muoni misurati Nδ diminuirà progressivamente all’aumentare dell’angolo di inclinazione θ ovvero alla lunghezza sδ rispetto a quelli misurati allo zenit Nz che sono proporzionali ai muoni in alta quota N0.
Il modello previsto per una geometria non corretta per gli effetti relativistici si può scrivere con questa relazione:

Nδ=k∙Nz∙e^{(-λ sδ/v)}

Invece lo stesso modello previsto e corretto per gli effetti relativistici si può scrivere così:

Nδ=k∙Nz∙e^{(-λ s(δ,r)/v)}

Queste due funzioni le possiamo evidenziare subito in un grafico, da notare che lo stesso grafico si può ottenere con qualsiasi valore di energia cinetica scelta per i muoni. In seguito la prova della validità degli effetti relativistici consiste nel confrontare sullo stesso grafico l’andamento di queste funzioni con le misure reali. Per avere un confronto diretto in un singolo grafico tuttavia bisognerà normalizzare i dati trasformandoli in percentuale.

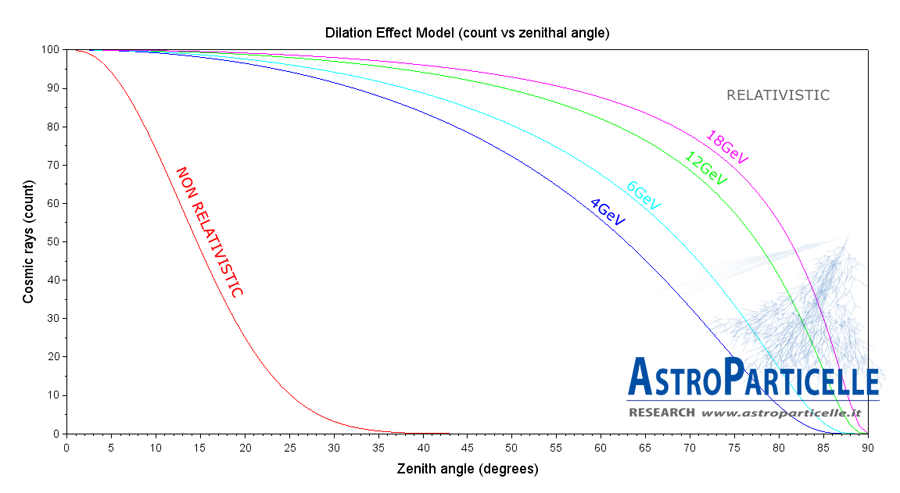
Modello applicato a muoni per 4, 6, 12 e 18 GeV

Le misure e i risultati

Le misure sono state impostate per ottenere un valore di muoni allo zenit Nz e valori a diversi angoli di inclinazione, ovvero per θ da 5° a 85° a step di 5° alla volta per un totale di 18 misurazioni durate 30 minuti ciascuna. Sono stati utilizzati due rivelatori di muoni (un modello AMD11 e un modello AMD5), come si evidenzia dal grafico di figura 3, il modello non relativistico indica che già con angolo di inclinazione pari a 40 gradi, il flusso dei muoni si dovrebbe azzerare, mentre le misure reali indicano che è ben oltre il 50%. La linea tratteggiata indica l’intensità dei muoni attesa, secondo la legge del coseno quadrato vista in precedenza.

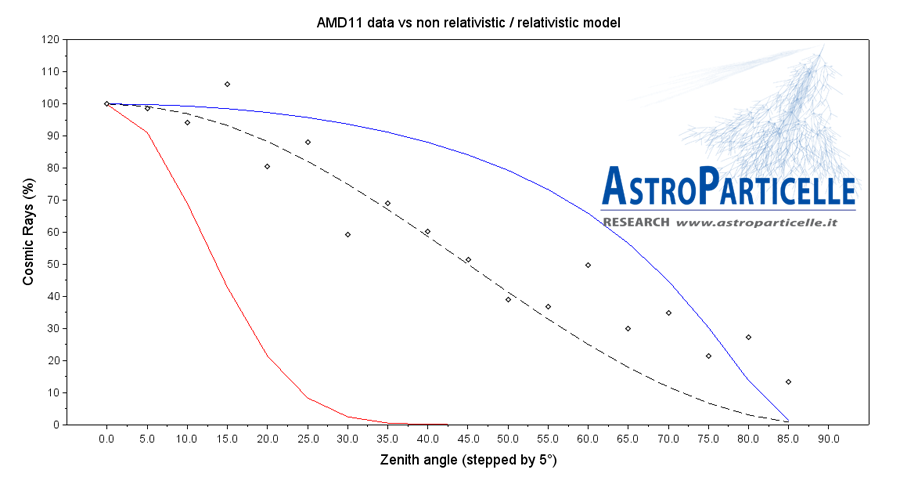
Prima misura con il rivelatore AMD11, i dati seguono il modello relativistico.

Con il secondo rivelatore i dati sono più sparpagliati perché ha una superficie di rivelazione inferiore e servirebbero tempi di misura più lunghi. In qualsiasi caso i dati seguono sicuramente e di nuovo l’andamento relativistico piuttosto che quello non relativistico.

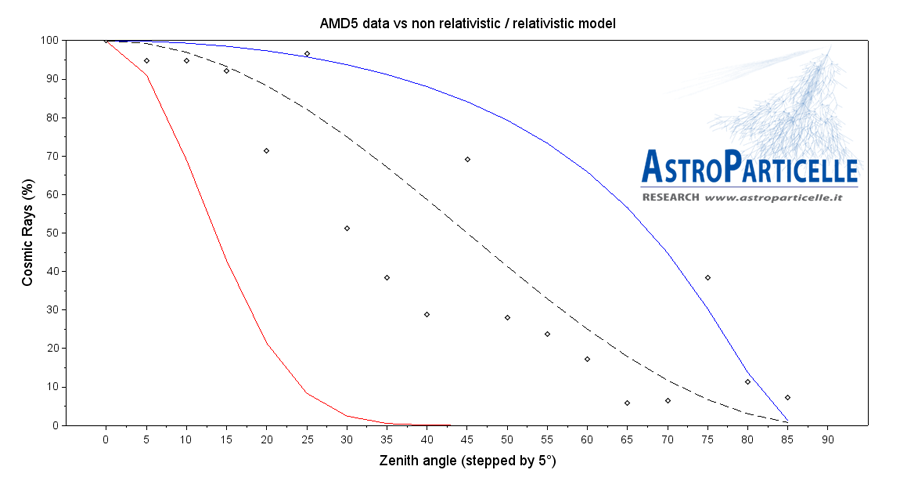
Misure con il rivelatore AMD5, i dati confermano il modello relativistico, nonostante siano più diffusi per mancanza di 'statistica'.

Conclusione

Il modello matematico può essere sicuramente sviluppato anche in altri modi, ma questo è piuttosto semplice e intuitivo, esso funziona con qualsiasi tipo di rivelatore e fornisce gli stessi risultati indipendentemente dal tasso di acquisizione (conteggio) dello strumento stesso. Questa è un'esperienza che in qualche modo mostra e convalida l'effetto di contrazione sulle lunghezze previsto dalla teoria della relatività speciale. L'esperimento si aggiunge alla lunga lista delle numerose attività che si possono ottenere con un semplice rivelatore di raggi cosmici come l’AMD5 e introduce ai numerosi aspetti della fisica sperimentale moderna, senza avere la necessità di un complesso apparato di laboratorio. Per questo motivo una tale esperienza è sicuramente adatta e utile anche alle scuole secondarie superiori.

Marco Arcani

Per una descrizione più formale vedere questo PDF

To the top